计算相比，光学计算以其固有的并行解决能力、高计算速度和低损耗在实现数学运算和图像处理方面慢慢的受到重视。特别是，光学微分操作允许对目标物体进行边缘检测，使物体特征

  一般来说，实现光学空间模拟微分有两种方法。根据傅里叶光学知识，传统的4f滤光系统能在傅里叶域对图像微分，但这种系统体积较大，难以实现紧凑的集成和小型化。近年来，超构表面这种人工光子结构可以有明显效果地地控制和灵活地操纵光场，不但可以应用于多功能全息、光谱成像、光传感、量子纠缠等领域，而且为实现图像的光学微分操作和边缘检测提供了强大的平台。利用表面等离激元共振、光子自旋霍尔效应和Pancharatnam-Berry相位能轻松实现超构表面微分器。然而，大多数方法都局限于一维或单一方向的微分，有些方法还需要额外的组件来完成，或者由于相关结构的光学响应有限而导致低NA，或只能在窄带情况下工作，这样一些问题都极大地限制了微分器的实际应用。

  针对上述实际挑战，研究人员利用超构表面在空域直接实现拉普拉斯微分算子，这种微分算子本质是一种具有各向同性能力的，能够使图像低频分量被滤除，而高频分量被保留，最终获得图像各个方向的边缘信息。这种光学特性能够最终靠具有环形偶极共振的超构表面来实现，原因是在正入射对称系统中，环形偶极共振通常被认为是非辐射暗模式，这有助于在这样的一种情况下获得接近零的透过率。当引入斜入射时，系统的对称性被打破，环形偶极共振会耦合出去，进而影响光谱传输特性。基于此原理，研究人员设计了单层硅方形孔超构表面，通过选择正真适合的结构参数，这种超构表面能够在近红外波段的1155nm处激发低Q值的环形偶极共振，并且其透射光谱在正入射下为零，随着入射角度的增大，透射光谱强度逐渐升高。

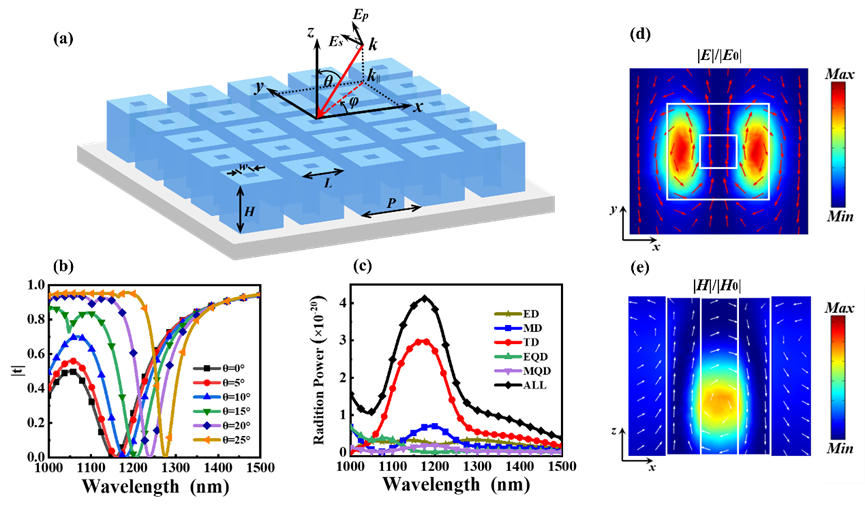
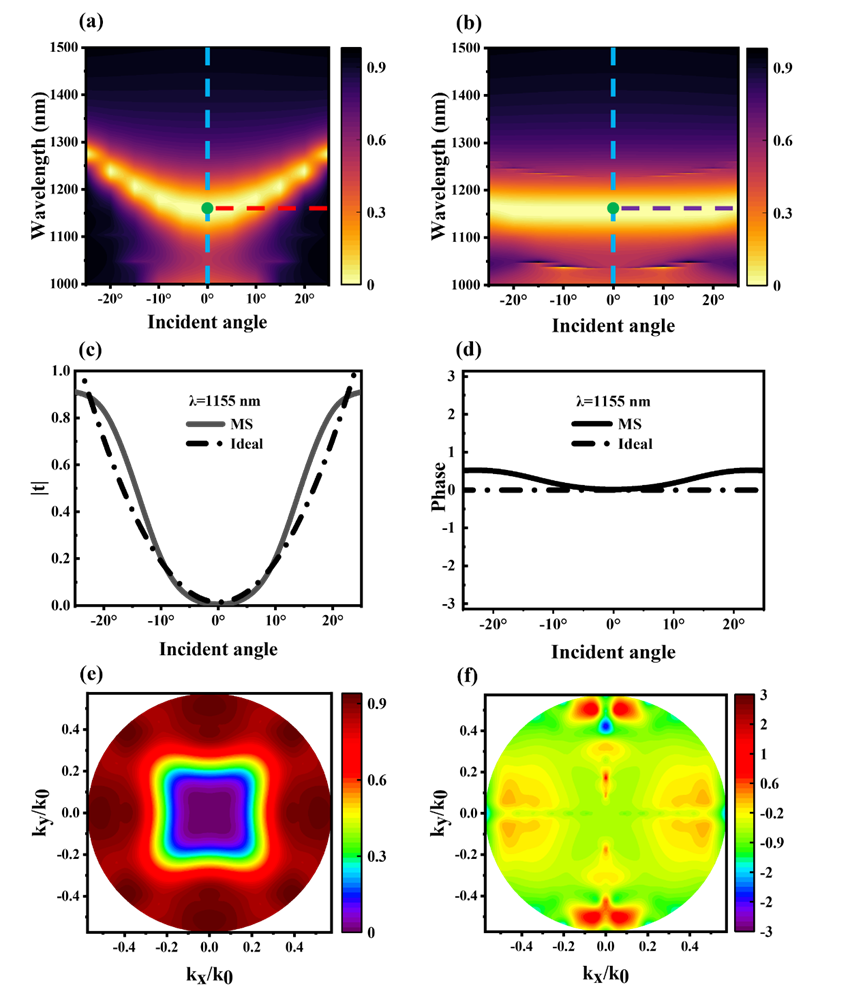
  为进一步验证方形孔超构表面透射光谱和入射角度的具体关系以及入射偏振态的影响，研究人员分析了P偏振光和S偏振光下透射光谱的特性，如图3所示。表明所设计的方形孔超构表面可以在P偏振光下得到光学拉普拉斯运算所需的光学传递函数，并使得该函数在各个方位角关于入射角满足二次关系，从而在空间域中可以直接实现二维二阶微分。

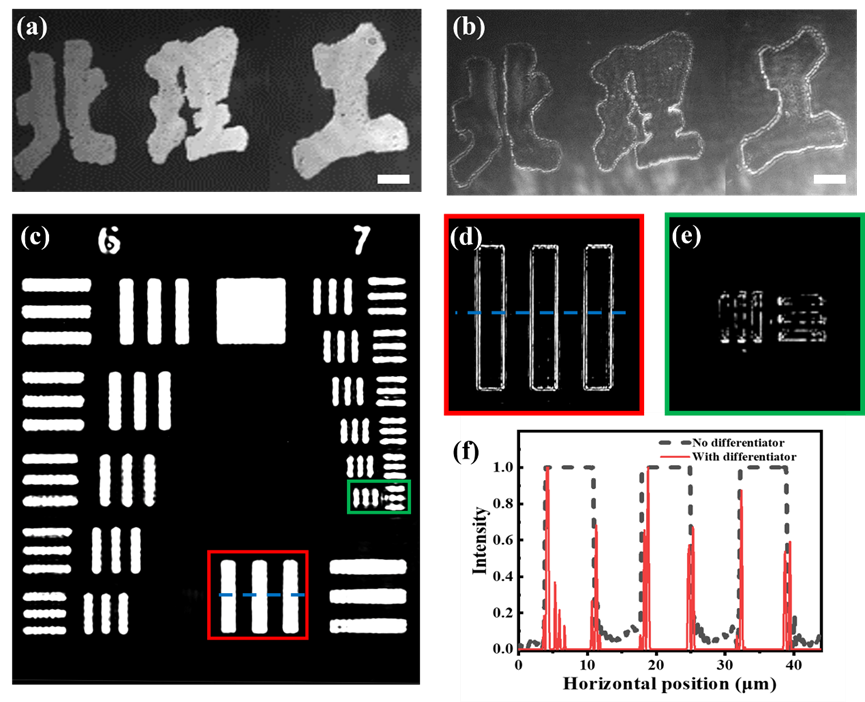
  实际实验结果如图4所示，所设计的拉普拉斯微分器可以在空域直接对“北理工”三个汉字图像完成二阶二维边缘检测，使得汉字的每个边缘周围形成两条紧密间隔的线条。同时，通过测试这种拉普拉斯微分器对标准分辨率板的成像效果，表明其能分辨出第7组第6个元素的线宽，相当于其至少可以对线μm的目标物体完成二阶二维边缘检测，实验结果与预期吻合良好。

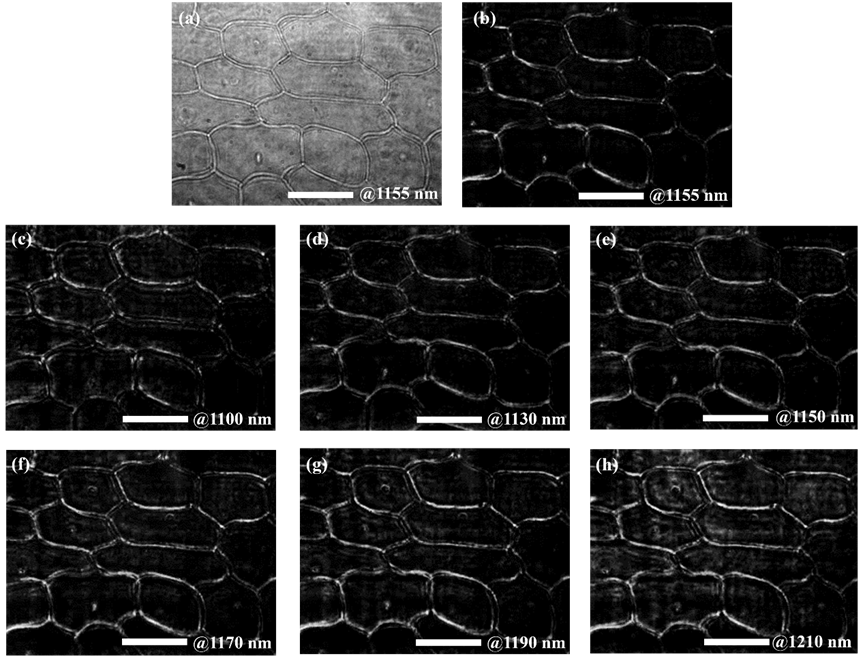
  随后，为了验证所设计的拉普拉斯微分器的宽带特性，研究成员在1100nm到1210nm范围内对未染色的洋葱表皮细胞进行了微分成像实验，如图5所示。当光源直接照射洋葱表皮细胞时，相邻洋葱表皮细胞的边界无法区分，而当加入方形孔超构表面拉普拉斯微分器后，能清楚地看到洋葱表皮细胞的完整边缘和轮廓。这将使透明细胞易于识别，极大地促进了生物学研究中细胞形态和行为模式的观察。

  研究团队提出的硅方形孔超构表面不仅仅可以在透射模式下支持角度选择的TD共振，还能够在实空间中得到拉普拉斯微分算子。这种光学特性能应用于数学计算和图像处理领域，分别实现微分运算和二维二阶图像边缘检测。同时，由于环形偶极共振的低Q值特性，能够有效拓宽实际在做的工作波长。这种轻薄的方形孔超构表面拉普拉斯微分器可以与现有的显微成像系统很好地集成，以高速、并行、实时和低功耗的方式完成大量的数据处理，为未来的无人驾驶、机器视觉和生物医学成像等提供坚实的基础。

  原文标题：基于环形偶极共振超构表面的拉普拉斯微分器，可用于光学成像、机器视觉等领域

  文章出处：【微信号：MEMSensor，微信公众号：MEMS】欢迎添加关注！文章转载请注明出处。

  显微镜分辨率极限(200nm)的显微镜，技术原理主要有受激发射损耗显微镜技术和光激活定位显微镜技术。 管中亦可窥豹——受激发射损耗显微镜 传统

  ”，近期成功通过IPO审核，准备在科创板上市。该公司计划募资18亿元，主要

  光伏高端装备研发生产总部基地项目、半导体及光伏高端设备研发制造基地项目，以及补充流动资金。

  信号分析和系统理论领域。虽然它们在数学定义和应用上有所差异，但它们之间有紧密的联系和相互依存的关系。 首先，我们先介绍一下傅里叶变换和

  极限 /

  光伏高端装备研发生产总部基地项目、半导体及光伏高端设备研发制造基地项目和补充流动资金。 从

  科创板IPO！三年营收翻涨近30倍，募资18亿建设半导体设备研发基地等

  科创板IPO！三年营收翻涨近30倍，募资18亿建设半导体设备研发基地等 /

  科创板IPO！三年营收翻涨近30倍，募资18亿建设半导体设备研发基地等

  科创板IPO！三年营收翻涨近30倍，募资18亿建设半导体设备研发基地等 /

  技术在许多领域中得到了广泛应用，其中之一便是物体三维重建。物体三维重建技术是一种通过计算机

  的物体三维重建技术研究 /

  变换是通过一种特定的方法将时域中的一个信号转化为复频域中的一个函数，从而使得复杂的

  方程等可以变得更简单、易于求解。因此，它在电路分析中的应用十分普遍，有助于

  变换公式是数学中非常非常重要的一种变换方式，它的应用领域十分普遍，包括在信号

  、控制理论、电路分析等领域大范围的应用。在这些应用中，频移是一个常见的操作，即将信号在频域上移动某个频率。

  轮廓仪是基于白光干涉技术，结合精密Z向扫描模块、3D 建模算法等快速、准确测量物体

  变换、Python 和 SymPy 以串联 RLC 电路为例简化电路分析的数学运算。 研究电路可能是一个非常滑坡。 在不知不觉中，你已经深入

  空间中的二阶电路 /

  【Longan Pi 3H 开发板试用连载体验】给ChatGPT装上眼睛，并且还可以语音对线，项目开发环境搭建

  【Longan Pi 3H 开发板试用连载体验】给ChatGPT装上眼睛，并且还可以语音对线，系统基础配置